5-demicubic honeycomb
| Demipenteractic honeycomb | |
|---|---|
| (No image) | |
| Type | uniform honeycomb |
| Family | Alternated hypercubic honeycomb |
| Schläfli symbol | h{4,3,3,3,4} |
| Coxeter-Dynkin diagram | |
| Facets | {3,3,3,4} h{4,3,3,3} |
| Vertex figure | Rectified pentacross |
| Coxeter group | 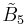 [4,3,3,31,1] [4,3,3,31,1]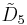 [31,1,3,31,1] [31,1,3,31,1] |
The 5-demicube honeycomb, or demipenteractic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 5-space. It is constructed as an alternation of the regular penteractic honeycomb.
It is the first tessellation in the demihypercube honeycomb family which, with all the next ones, is not regular, being composed of two different types of uniform facets. The penteracts become alternated into demipenteracts h{4,3,3,3} and the alternated vertices create pentacross {3,3,3,4} facets.
Its vertex arrangement, the 40 vertices of a rectified pentacross, is called the D5 lattice.[1]
Contents |
Kissing number
This tessellation represents the most dense known 4-sphere packing in 5-dimensions, with a kissing number of 40. Each vertex of this polytope represents the center point for one of the 40 4-spheres, and the central radius, equal to the edge length exactly fits one more 4-sphere.[2]
See also
- Cubic honeycomb
- Alternated cubic honeycomb
- Demitesseractic honeycomb
- Demipenteractic honeycomb
- Demihexeractic honeycomb
- Demihepteractic honeycomb
- Demiocteractic honeycomb
- Uniform polytope
References
- ^ http://www2.research.att.com/~njas/lattices/D5.html
- ^ Sphere packings, lattices, and groups, by John Horton Conway, Neil James Alexander Sloane, Eiichi Bannai [1]
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- pp. 154–156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}, ...
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
External links
- Olshevsky, George, Half measure polytope at Glossary for Hyperspace.